Vorlesung 2

主要内容

• Probabilities and ensembles 概率与总体
• 概率的运算
• 课后练习题

概率与总体

**总体（ensemble）**x 是一个3- 元组（triple）(x, Ax ,Px)，其中 x 是一个随机变量，AX 是构成这些变量的集合 Ax = {a1,a2,a3,…ai}, PX是相对应与每个变量的概率的集合 Px ={P1,P2,P3…}.

他们的之间的关系为： $$\sum_{a \epsilon A_{x} }^{}P(x=a) = 1 $$

对于单个元素，它的概率表示为： $$ P(x=a1) = P(a1) = P1 $$

子集的概率，假如 T 是 Ax 的一个子集，则子集T的概率可以表示为： $$ P(T) =P(x\epsilon T)= \sum_{a \epsilon T }^{}P(x=a)$$

联合概率，XY是一个总体，它的结果与两个随机变量 x,y 有关，其中x属于 Ax ={a1,a2,a3…}， y 属于Ay = {b1,b2,b3…}，我们称这样的总体为联合总体，把P(x,y)称为 x 和 y 的联合概率。

边缘概率，我们可以从连个概率 P(x,y)中得到边缘概率P(x) $$ P(x=a_{i}) = \sum_{y\epsilon A_{y}}P(x=a_{i},y) $$

类似的，可以得出 y 的边缘概率为： $$ P(y) = \sum_{x \epsilon A_{x}}P(x,y) $$

条件概率，P(x=a1/y=b1)读作在给定 y = b1 的条件下，x = a1 的概率。 $$ P(x=a_{i}|y=b_{j}) = \frac{P(x=a_{i},y=b_{j})}{P(y=b_{j})}, P(y=b_{j})\neq 0$$

我们可以发现，条件概率P(x/y) 是由 联合概率 P(x,y) 除以 边缘概率 P(y) 得出。

概率的运算

关于概率的运算常用的法则主要有： 乘法律，加法律，贝叶斯定理。

乘法律 $$ P(x,y) = P(x|y)P(y) = P(y|x)P(x) $$ 该法则也称为链式法则。

加法律 $$ P(x) = \sum_{y}P(x,y) = \sum_{y}P(x|y)P(y) $$

贝叶斯定理 $$ P(x|y) = \frac{P(y|x)\cdot p(x)}{P(y)} = \frac{P(y|x)\cdot p(x)}{\sum_{x'}P(y|x')\cdot P(x')} $$

独立性
如果变量 x , y 相互独立，那么联合概率 $$ P(x,y) = P(x)P(y) $$

练习题

例1 小明去做了新冠检测，用变量a表示健康状态，患病( a = 1 )，不患病( a=0 )，b表示检查结果，阳性(b=1)，阴性（b=0), 假设检测结果95%是可靠的，普通人患有新冠的概率是 1% ，那当检测结果呈阳性时，小明患有新冠的概率是多少？

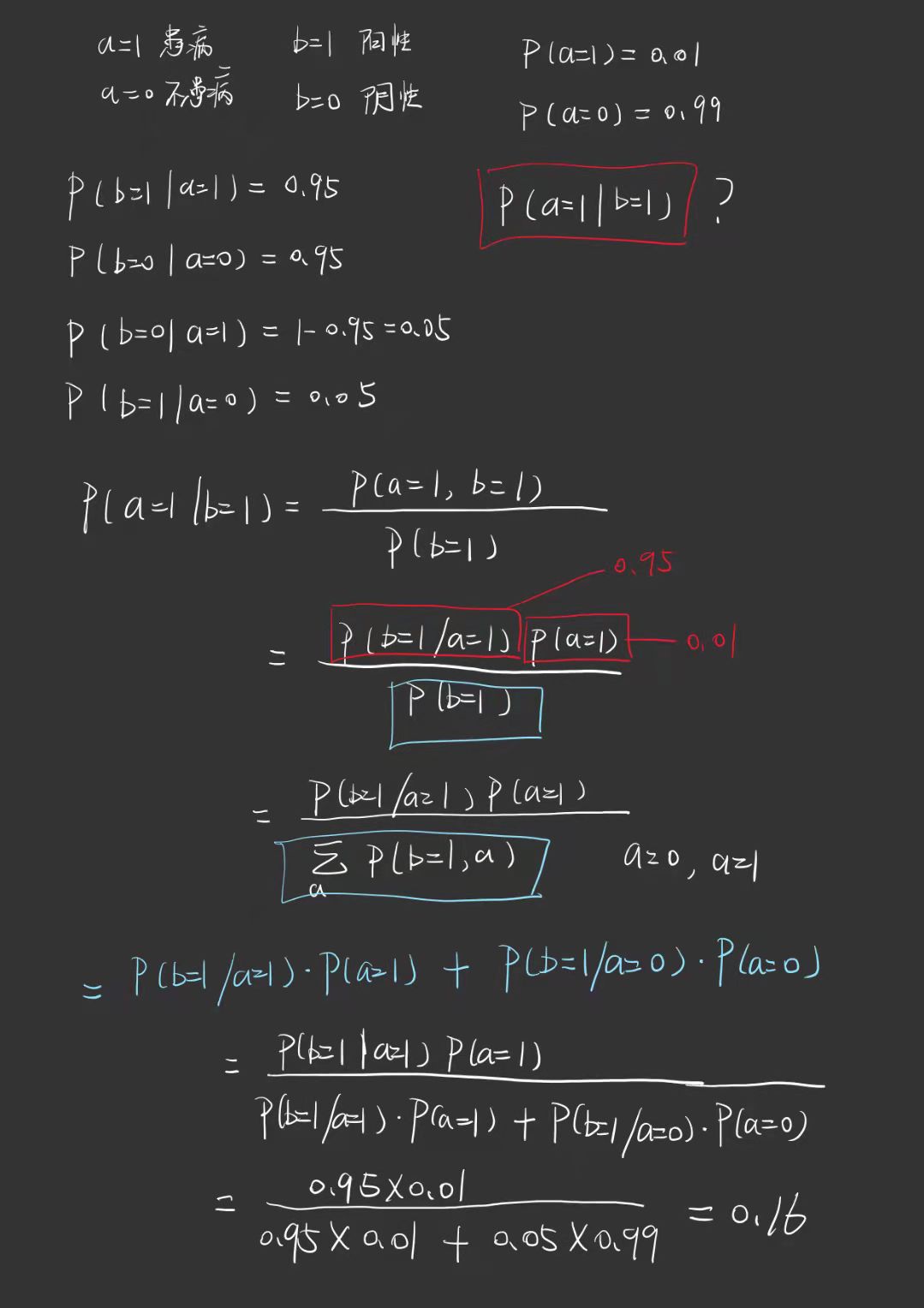
例2 共有11个罐子，标记为 u 属于 {0,1,2,3,…10}, 每个罐子中有10个球,u号罐子中有u个黑球和 10-u 个白球。小明随机选择一个罐子有放回的抽球 N 次，结果是 b 次是黑球，N-b次是白球，假如一共抽了 N=10 次，其中抽到 b=3 次黑球，N-b=7 次 白球，那么小明选择的罐子是 u 的概率是多少？ u 等于多少时概率最大？