Vorlesung 1
主要内容
- Binomial distribution 二项分布
- Permutations 排列组合
- Poisson distribution 泊松分布
- binary entropy function以二为底的熵函数
- Hamming code 汉明码
- Binomial distribution 二项分布
Wir haben eine münze, die auf Kopf fällt mit Wahrscheinlichkeit f. Wie hoch ist die Wahrscheinlichkeit für r mal Kopf bei N münze werfen?
一枚硬币抛正面的概率是f,那么抛 r 次,有 N 次是正面的概率是多少?
二项分布公式:
$$ P(r|N,f) = \binom{N}{r} f^{r}(1-f)^{N-r} $$
该分布的均值
$$ E(r) = \sum_{r=0}^{N}P(r|N,f)r = Nf $$
方差
$$ Var[r] = \sum_{r=0}^{N}P(r|f,N)r^{2}-(E[r])^{2} = N(1-f)f$$
- 排列组合的写法
$$ \binom{N}{r} = \frac{N!}{r!(N-r)!} $$
- 使用泊松分布推导X! 和 排列组合公式 的近似值
均值为 λ 的泊松分布公司为: $$ P(r|\lambda ) = e^{-\lambda} \frac{\lambda^{r}}{r!} $$
当 λ 较大时,可使用λ的高斯分布近似取得 $$ e^{-\lambda} \frac{\lambda^{r}}{r!} \simeq \frac{1}{\sqrt{2\pi \lambda }}e^{-\frac{(r-\lambda )^2}{2\lambda }}$$
当 r = λ 时 ,代入得: $$ e^{-\lambda} \frac{\lambda^{\lambda }}{\lambda !} \simeq \frac{1}{\sqrt{2\pi \lambda }} $$
可推出: $$\lambda !\simeq \lambda ^{\lambda }e^{-\lambda }\sqrt{2\pi \lambda } $$
所以,阶乘 X! 的近似值可写成: $$ x!\simeq x ^{x }e^{-x }\sqrt{2\pi x } $$
对 X!取对数,可得: $$ \ln x! \simeq x\ln x - x+\frac{1}{2}\ln 2\pi x $$
将上式应用于排列组合上,可得: $$\ln \binom{N}{r} = \ln\frac{N!}{(N-r!)r!} \simeq (N-r)\ln\frac{N}{N-r}+ r\ln\frac{N}{r}$$
此处我们引入 以2为底的熵函数
$$ H_{2}(x) = x \log \frac{1}{x} + (1-x)\log \frac{1}{(1-x)} $$
则排列组合取对数后可写为: $$ \ln \binom{N}{r} \simeq NH_{2}(r/N) $$
所以,排列组合公式的近似值 可写成: $$ \binom{N}{r} = 2^{NH_{2}(r/N)} $$
重复码
在信号传输过程中,往往会出现差错,为了减少差错,我们会加入一些有用的冗余信息,最简单的办法就是多传几个,类似于“重要的事情说三遍”,这就是重复码,而在译码过程中,则采用少数服从多数的办法来获取信源信息。
如:重复码 R3 ,重复三次。
| 源序列 | 发送序列 |
|---|---|
| 0 | 000 |
| 1 | 111 |
重复码的译码是少数服从多数的原则,如R3的译码表:
| 接收序列 | 译码序列 |
|---|---|
| 000 | 0 |
| 001 | 0 |
| 010 | 0 |
| 011 | 1 |
| 100 | 0 |
| 101 | 0 |
| 110 | 1 |
| 111 | 1 |
练习
假设传输过程中的误差为f. 使用R3(重复3次)和R5(重复5次)的编码方式传输,出错的概率分别为多少?
重复3次的概率为: $$ P = f^{2}(1-f) \binom{3}{2} + f^{3} \binom{3}{3}$$
重复5次的概率为: $$ P = f^{3}(1-f)^{2} \binom{5}{3} + f^{4}(1-f)\binom{5}{4} + f^{5} \binom{5}{5}$$
类似的可得出重复 N 次时,重复码的差错概率是:
$$ P_{b}=\sum_{n = (N+1)/2}^{N}\binom{N}{n}f^{n}(1-f)^{N-n}$$
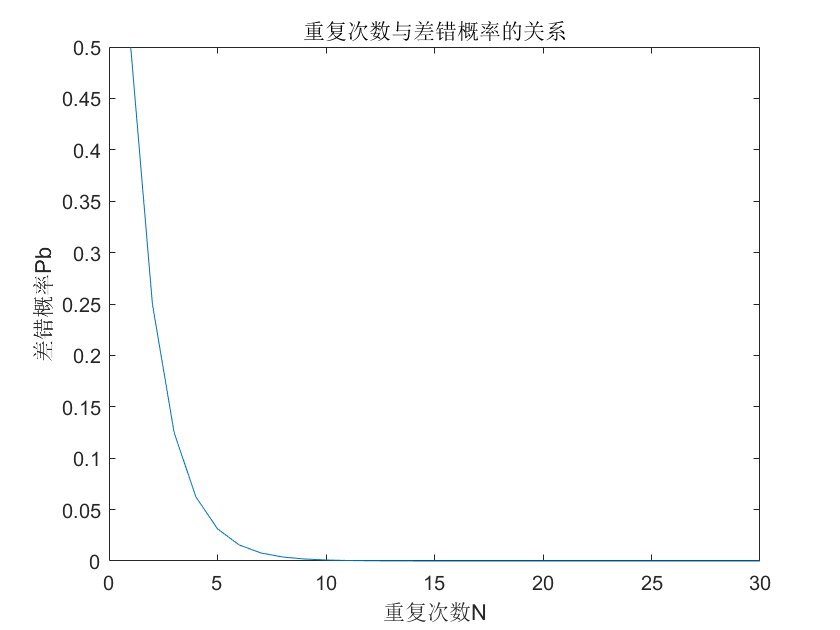
显然,重复次数越多,误差越低,使用matlab画图可得:
f = 0.5 ; %误差
T = [1:30]; % 实验次数,假定为30
t = length(T);
Pb = zeros(1,t) ;% 差错概率,初始值设为0
for N = 1:t
for n= ceil((N+1)/2) : N
Pb(N) = nchoosek(N,n) * power(f,n) * power(1-f,N-n);
end
end
plot(Pb);
title('重复次数与差错概率的关系')
xlabel('重复次数N')
ylabel('差错概率Pb')